ANSWER
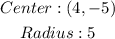
Step-by-step explanation
We want to find the center and radius of the circle with the given equation:
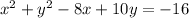
To do this, we have to write the equation in standard form:

where (h, k) = center
r = radius
To do this, complete the square for both x and y variables of the equation.
Let us do that now:

Finally, factorize both the x and y variables:

Therefore, the center and radius of the circle are:
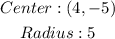
That is the answer.