Consider that the data given is discrete in nature.
The mean of the discrete data is calculated as,

Thus, the mean weight is 11.125 pounds.
Now, arrange the data in increasing order,
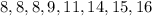
Since there are 8 data points i.e. an even no. of data points, the median is given by the arithmetic mean of the two middle-most data points.
Here, the two middle values are 9 and 11,
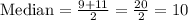
Thus, the median weight is 10 pounds.