Given:
The person plans to retire in, x = 20 years.
The objective is to select the correct plan and to choose the correct plant if the person decides to retire more than 20 years.
Step-by-step explanation:
Let's check the amount received at 20 years for three different plans.
To retire at 20 years;
In plan A:
At x = 20 in the given function,
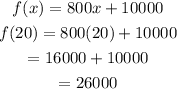
Thus, the amount received from plant A is 26000.
In plan B:
From the given table, at x = 20 the amount received in plan B is 36500.
In plan C:
From the given quadratic function, at x = 20 the amount received in plan C is 24,403.2.
Since, by comparing all the three results, plan B obtains more amount compared to other plans.
To retire after 20 years:
If the person plans to retire longer than 20 years, then plan A gives a constant increase in amount after n number of years as it is a linear function.
But plan B is an increasing exponential function. So with increase in n number of years, the amount will also increase after n years.
Considering the graph of plan C, it appears to be a constant amount after successive 5 years interval.
Hence,
If the person retire at 20 years, he should choose plan B.
If the person plans to retire longer than 20 years, his best option is to keep the same plan.