Question

The doubling time of a population of bees is 9 days. If there are initially 300 bees, how many bees will there be in 26 days?

Answer 1

Since each nine days the population doubles that means that after nine days we will have:

`600`

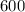
after 18 days we will have:

`1200`

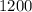
and so on.

This means that we can model the population by a function of the form:

`y=A\cdot B^x`

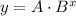
where A is the inital population and B is the growth.

Now we know that the initial population is 300 and that it doubles each nine days, that means that B has to be two. To correctly model the population we need to make sure that this happens every nine days that means that the x should be divided by nine; therefore the function modeling the population is:

`y=300(2)^{(x)/(9)}`

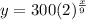
where x represents the days.

Once we know the function we just plug the value we need, in this case we need the population after 26 days, this means that x=26, then we have:

`\begin{gathered} y=300(2)^{(26)/(9)} \\ y=2222.1 \end{gathered}`

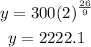
Therefore we conclude that the population of bees after 26 days is approximatey 2222