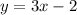Question

Given the equation below , find (dy)/(dx); - 36x ^ 10 + 9x ^ 36 * y + y ^ 3 = - 26

Answer 1

We have the expression:

`-36x^(10)+9x^(36)y+y^3=-26`

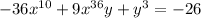
And they ask for the differentiation of y with respect to x, then we need to assume based on the implicit derivate to y as y(x). Then we derivate both sides as:

`(dy)/(dx)(-36x^(10)+9x^(36)y+y^3)=(dy)/(dx)(-26)`
`-360x^9+324x^(35)y+9x^(36)\frac{\text{ dy}}{dx}+(3y^2dy)/(dx)=0`

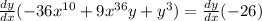
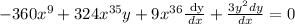
We ordinate the expression and take factor comun the differentiation in order to leave it alone:

`(9x^(36)dy)/(dx)+(3y^2dy)/(dx)=360x^9-324x^(35)y`
`(dy)/(dx)(9x^(36)+3y^2)=360x^9-324x^(35)y`
`(dy)/(dx)=(360x^9-324x^(35)y)/(9x^(35)+3y^2)=(12x^9(10-9x^(26)y))/(3x^(35)+y^2)`

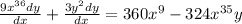
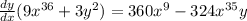
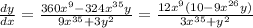
Then, we can say:

`(dy)/(dx)=(12x^9(10-9x^(26)y))/(3x^(35)+y^2)`

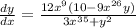
To obtain the tangent line we know that the slope of this tangent is the derivate evaluated in the given point, then:

`m=(dy)/(dx)(1,1)=3`

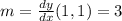
And we use the standard formula for a line:

`y-y_0=m(x-x_0)`

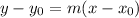
We reply our values:

`y=3x-3+1`
`y=3x-2`

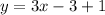
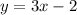
Then the tangent line that pass through the curve in the point (1,1) is:

`y=3x-2`