We assume the next variables
x=number of games
y= cost per one game
the inequality is
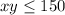
the sign equal less than is used in this inequality because the total cost can't be more than 150
in order to know how many games she can buy, we need to isolate x

If y= 20 for example
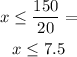
she can buy 7 games if the cost per game is 20