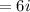Given the expression:
![\sqrt[]{-3}\cdot\sqrt[]{12}](https://img.qammunity.org/2023/formulas/mathematics/college/38w834s00h5bd8lmsmila2c76m0dsj1i9g.png)
You need to remember the following property:
![\sqrt[n]{b^{}}\cdot\sqrt[n]{a}=\sqrt[n]{ba}](https://img.qammunity.org/2023/formulas/mathematics/college/5vz7d4miv0rpshrr1jqb6vgv082zsx5zpq.png)
Where "n" is the index of the root and "b" and "a" are Radicands.
Then, since the roots given in the exercise are the same, you can multiply the Radicands:
![=\sqrt[]{(-3)(12)}=\sqrt[]{-36}](https://img.qammunity.org/2023/formulas/mathematics/college/cemvii2wus412c3wbnfhgh10a1tcku5j9u.png)
Notice that the number inside the square root is negative. Then, you need to remember the following:
![\sqrt[]{-1}=i](https://img.qammunity.org/2023/formulas/mathematics/high-school/6auedmvsax8nlo4hpms2kngcv15a6lmlel.png)
Therefore, in order to simplify it, you need to take the square root of 36 and write the Imaginary Unit "i" next to it:
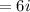
Hence, the answer is: