Question

A ball bounces to a height of 6.7 feet on the first bounce. Each subsequent bounce reaches a height that is 81% of the previous bounce. What is the height, in feet, of the sixth bounce? Round your answer to the thousandths place. 1.892 ft 2.336 ft 2.650 ft 5.427 ft

Answer 1

`\text{ 2.336 ft }(\text{option B)}`

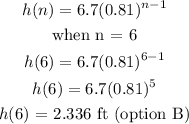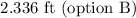
Step-by-step explanation:

On the 1st bounce, height = 6.7 feet

We were not given the inital height of the ball before the 1st bounce

2nd bounce:

height = 0.81 of the previous bounce

height = 0.81(6.7)

3rd bounce:

height = 0.81 of the previous bounce

previous bounce = 0.81(6.7)

height = 0.81(0.81 × 6.7)

We can derive a formula for the nth bounce:

`\begin{gathered} \text{height = 6.7(0.81)}^{n\text{ - 1}} \\ h(n)\text{ = 6.7(0.81)}^{n\text{ - 1}} \\ To\text{ check:} \\ \text{when n = 1} \\ h(1)\text{ = 6.7(0.81)}^{1\text{ - 1}}\text{ = 6.7 ft} \end{gathered}`

For the sixth bounce, height:

`\begin{gathered} h(n)=6.7(0.81)^(n-1) \\ \text{when n = 6} \\ h(6)=6.7(0.81)^(6-1) \\ h(6)=6.7(0.81)^5 \\ h(6)\text{ = 2.336 ft }(\text{option B)} \end{gathered}`