Question

Instructions: Identify how the parent function =2 was transformed to create the given function.

Answer 1

Given:

`The\text{ parent function is }y=x^2.`
`\text{The new function is y =-3x}^2-7`

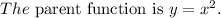
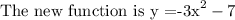
Required:

We need to find the type of transformation of the new function.

Step-by-step explanation:

The parent function is multiplied by the value 3 to get a new function.

`y=3x^2`

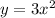
Recall that to stretch the function, multiply by a fraction between 0 and 1.

To compress the function, multiply by some number greater than 1.

Here we multiplied the given function by 3 so the transformation is stretch.

The negative sign of 3 indicates the flection of the function.

`y=-3x^2`

We get the new function by subtracting 7 from the stretched function.

`y=-3x^2-7`

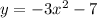
By subtracting 7, the new function moves down vertically.

Consider the graph of both functions.

Final answer:

Vertically stretch.

Vertically down 7 units.