Question

Find all points (x,y) on f(x)=x^3-7x+3 where the slope of the tangent line is 41

Answer 1

To find the points on the function:

`f(x)=x^3-7x+3`

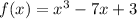
where the slope of the tangent line is 41 we need to remeber that the slope of the tangent line is given by the derivative; then we need to find it:

`\begin{gathered} (df)/(dx)=(d)/(dx)(x^3-7x+3) \\ =3x^2-7 \end{gathered}`

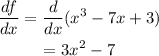
Now we equate the derivative to 41 to find the values of x where this happens:

`\begin{gathered} 3x^2-7=41 \\ 3x^2=48 \\ x^2=(48)/(3) \\ x^2=16 \\ x=\pm\sqrt[]{16} \\ x=\pm4 \end{gathered}`

Hence the points on f(x) where the tangen line has an slope of 41 happen at x=-4 and x=4. Now that we know the x component to find the points we plug them in the function:

`\begin{gathered} f(-4)=(-4)^3-7(-4)+3 \\ f(-4)=-64+28+3 \\ f(-4)=-33 \end{gathered}`

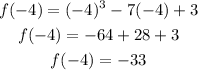
Then the first point is (-4,-33).

For x=4 we have:

`\begin{gathered} f(4)=(4)^3-7(4)+3 \\ f(4)=64-28+3 \\ f(4)=39 \end{gathered}`

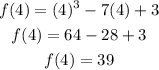
Then the second point is (4,39)

Therefore the two points where the tangent line has a slope of 41 are (-4,-33) and (4,39)