Question

#20 “Summer Savings”A student invests the majority of her summer job earnings into an investment account. She has $800 to invest and the account she has chosen compounds continuously at 3%. Hint: (Use the compound interest formula: where a represents the initial amount, ⎛r represents the interest rate as a decimal, n represents the number of times y = a 1+ compounded in a year, and x represents time in years. ⎜⎝ n ⎟⎠a) Create a model to represent the balance of the investment account over time.b) What is the y-intercept and what does it represent?c) What will be the balance in 5 years?d) How does this investment account compare to anotheraccount that offers 3% compounded monthly over 5 years?

Answer 1

Step-by-step explanation

The compounded interest is given by the following expression:

`y=a(1+(r)/(n))^(nx)`

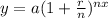
Where a=Principal=800, r=interest rate in decimal form=3/100=0.03 n=number of times compounded in a year = 360:

We assume 360 because the account is compounded continuously, the model would be as shown as follows:

`y=800(1+(0.03)/(360))^(360x)`

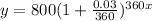
b) We can see that the y-intercept is at (0,800) and it represents the Initial Capital.

c) The balace in 5 years will be give by the following relationship:

`y=800(1+(0.03)/(360))^(360\cdot5)`
`y=800(1+(0.03)/(360))^(1800)`
`y=800\cdot1.1618`

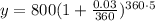
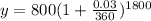
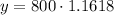
Multiplying numbers:

`y=929.46`

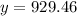
The balance in 5 years will be of $929.46

d) Comparing to another account compounded monthly, n=12:

`y=800(1+(0.03)/(12))^(12\cdot5)`
`y=800(1+(0.03)/(12))^(60)`
`y=800\cdot1.1616`

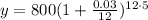
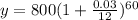
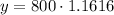
Multiplying numbers:

`y=929.29`

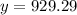
In conclusion, after 5 years, the investment will be almost the same, just a bit lower than continuously compounded.