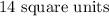Given the Kite ABCD.
We want to find the Area of the Kite.
Recall that the Area of a Kite can be expressed as;
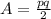
Where;
p and q are the diagonals of the Kite.
For the given Kite, the diagonals of the kite are;
AC and BD.
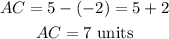
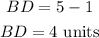
So,
p = AC = 7 units
q = BD = 4 units
Substituting into the formula, we have;
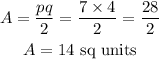
Therefore, the area of the Kite is;