Answer:
P = 0.000004
Step-by-step explanation:
The number of ways or combinations to select 4 cards from 52 cards can be calculated using the following equation:
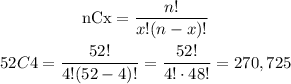
It means that there are 270,725 ways to select 4 cards out of 52.
Additionally, there are only 4 queens in the deck, so there is only one possibility where the 4 cards are queens. So, the probability that all 4 cards are queens is:
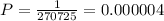
So, the answer is P = 0.000004