We start with the following statement:
A number that has exact two distinct factors is prime.
This is a conditional statement. Given the condition(or hypothesis) 'exact two distinct factors' we have a conclusion 'is prime'. The inverse of a conditional statement is when both the hypothesis and conclusion are negated; the “If” part or p is negated and the “then” part or q is negated.
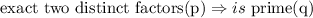
The inverse of the statement is given by NEGATING the hypothesis, implying in a negation of the conclusion of the previous statement.
The inverse would be:
If the number doesn't have exact two distinct factors the number is not prime.
Which is the second option.