Question

A sample of a radioactive isotope had an initial mass of 360 mg in the year 1998 and

decays exponentially over time. A measurement in the year 2004 found that the
sample's mass had decayed to 270 mg. What would be the expected mass of the
sample in the year 2011, to the nearest whole number?

Answer 1

193 mg

Explanation:

Exponential decay formula:

• 
  `A_t = A_0e^r^t`
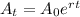
• where Aₜ = mass at time t, A₀ = mass at time 0, r = decay constant (rate), t = time

Our known variables are:

• 1998 to the year 2004 is a total of t = 6 years.
• The sample of radioactive isotope has an initial mass of A₀ = 360 mg at time 0 and a mass of Aₜ = 270 mg at time t.

Let's solve for the decay constant of this sample.

• 
  `270=360e^-^r^(^6^)`
• 
  `270=360e^-^6^r`
• 
  `(3)/(4) =e^-^6^r`
• 
  `\text{ln} ((3)/(4) )= \text{ln}(e^-^6^r)`
• 
  `\text{ln} ((3)/(4) )=-6r`
• 
  `r=-\frac{\text{ln}(3)/(4) }{6}`
• 
  `r=0.04794701`

Using our new variables, we can now solve for Aₜ at t = 7 years, since we go from 2004 to 2011.

Our new initial mass is A₀ = 270 mg. We solved for the decay constant, r = 0.04794701.

• 
  `A_t=270e^-^(^0^.^0^4^7^9^4^8^0^1^)^(^7^)`
• 
  `A_t=270e^-^0^.^3^3^5^6^2^9^0^7`
• 
  `A_t=193.01982213`

The expected mass of the sample in the year 2011 would be 193 mg.