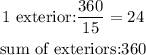In general, in the case of a regular polygon, the size of each interior angle is
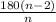
And the measure of each exterior angle is

1) A nonagon has 9 sides and its interior/exterior angles are
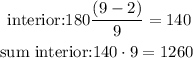
and
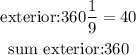
2) One of the interior angles of the polygon is 150°; thus,
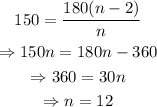
The number of sides of the fourth figure is 12 (dodecagon). The sum of its inner triangles is 12*150°=1800°. As for its exterior angles,
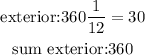
3) Since the regular polygon has 15 sides, it is called a pentadecagon.
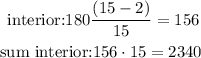
As for its exterior angles