Given: The graph of a quadratic equation as shown
To Determine: The equation of the graph
Solution
Let us determine the zeros
The zeros of the equation is given as the points where the curve cuts the x-axis
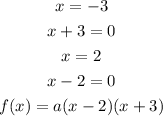
The y-intercept is
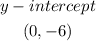
Substitute the coordinate of the y-axis to get the value of a
So,
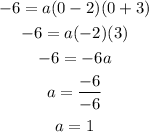
Hence the equation of the graph is
f(x) = 1(x + 3)(x -2)