Answer:
• (a)900 test scores
,
• (b)1350 test scores
Step-by-step explanation:
Part A
First, determine the number of test scores below Q2
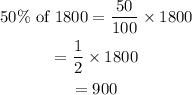
If a sample consists of 1800 test scores, 900 of them would be at or below the second quartile (Q2).
Part B
Next, determine the number of test scores above Q1.
Since 25% of the test scores are below Q1, 75% of the test scores will be above Q1.
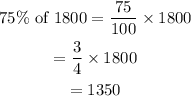
If a sample consists of 1800 test scores, 1350 of them would be at or above the first quartile (Q1).