Question

We a quadratic function in the vertex form f(x)=a(x-h)^2+k such that the graph of the function opens down and has a vertex at (5-5) and passes through the point (7,-9)The function is

Answer 1

f(x) = - (x - 5)² - 5

Step-by-step explanation:

The vertex form of the quadratic function is:

`\begin{gathered} f\mleft(x\mright)=a\mleft(x-h\mright)^2+k \\ \text{where (h,k) is the vertex} \end{gathered}`

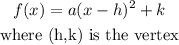
Given that it has a vertex at (5, -5),

(h,k)=(5,-5)

`\begin{gathered} f(x)=a(x-5)^2+(-5) \\ f(x)=a(x-5)^2-5 \end{gathered}`

Since it passes through the point (7,-9)

When x=7, f(x)=-9

`\begin{gathered} -9=a(7-5)^2-5 \\ -9=a*2^2-5 \\ -9+5=4a \\ -4=4a \\ a=(-4)/(4)=-1 \end{gathered}`

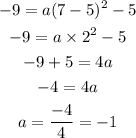
Therefore, the function is:

f(x) = - (x - 5)² - 5