Question

A weightless beam supports a weight of 266Ndown. Find FA up at 3.00 m from this weight andFB up on the other side of this weight at 5.00mfrom it. Draw the situation.

Answer 1

Given data:

* The weight supported by the weightless beam is W = 266 N.

* The distance of the force acting in an upward direction from the weight is,

`d_A=3\text{ m}`

* The distance of the force acting in an upward direction on the other side from the weight is,

`d_B=5\text{ m}`

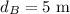
Solution:

The diagrammatic representation of the given case is,

The net moment about the weight on the beam (considering anticlockwise direction as positive and clockwise direction as negative is,

`\begin{gathered} m=-F_A* d_A+F_B* d_B \\ m=-F_A*3+F_B*5 \\ m=5F_B-3F_A \end{gathered}`

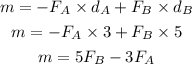
The beam balances the weight and the forces acting on the beam.

Thus, the net moment about the weight on the beam is zero.

`\begin{gathered} 5F_B-3F_A=0 \\ 5F_B=3F_A \\ F_B=(3)/(5)F_A\ldots\text{.}\mathrm{}(1) \end{gathered}`

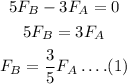
The net force acting along the vertical direction (taking upward direction as positive and downward direction as negative) is zero as there is no motion of the beam taking place in the vertical direction, thus,

`\begin{gathered} F_A+F_B=W \\ F_A+F_B=266\ldots\text{.}\mathrm{}(2) \end{gathered}`

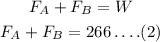
From (1) and (2) equations,

`\begin{gathered} F_A+(3)/(5)F_A=266 \\ (5+3)/(5)F_A=266_{} \\ (8)/(5)F_A=266 \\ F_A=(5)/(8)*266 \end{gathered}`

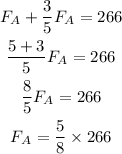
By solving,

`F_A=166.25\text{ N}`

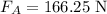
From the equation (1),

`\begin{gathered} F_B=(3)/(5)*166.25 \\ F_B=99.75\text{ N} \end{gathered}`

Thus, the value of force F_A is 166.25 N and F_B is 99.75 N.