1 Answer

Brpaz · Answer 1 · 2023-09-11T18:15:42+0000

The formula for getting the volume of a hemisphere is this:

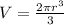
$V=(2\pi r^3)/(3)$

From this formula, we can solve for the radius then, the diameter of the hemisphere.

Let's plug into the formula above the given volume of the hemisphere.

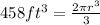
$458ft^3=(2\pi r^3)/(3)$

Let's now solve for the radius.

1. Cross multiply both sides of the equation.

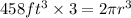
$458ft^3*3=2\pi r^3$
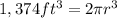
$1,374ft^3=2\pi r^3$

2. Divide both sides of the equation by 2π.

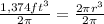
$(1,374ft^3)/(2\pi)=(2\pi r^3)/(2\pi)$
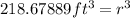
218.67889ft^3=r^3

3. Get the cube root on both sides of the equation.

$\sqrt[3]{218.67889ft^3}=\sqrt[3]{r^3}\Rightarrow6.0247ft=r$

Therefore, the radius of the hemisphere is approximately 6.0247 ft.

Since the diameter is twice the radius, then the diameter is:

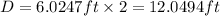
Therefore, the diameter of the hemisphere is approximately 12.0 ft.

Please log in or register to add a comment.