step 1
Find out the area of the circle
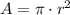
where
r=4 units
substitute
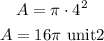
step 2
Find out the area of the sector
Remember that
The area of the complete circle subtends a central angle of 2pi radians
so
Applying proportion
Find out the area of the sector by a central angle of 2pi/3 radians
16pi/2pi=x/(2pi/3)
solve for x
x=8*(2pi/3)
x=16pi/3 unit2
the area of the sector is 16pi/3 unit2
step 3
Find out the circumference of the circle
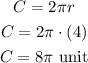
step 4
Find out the arc length by a central angle of 2pi/3 radians
Remember that
The circumference of the circle subtends a central angle of 2pi radians
so
Applying proportion
8pi/2pi=x/(2pi/3)
x=4*(2pi/3)
x=8pi/3 units
therefore
Verify each statement
N 1 -----> false
N 2 ----> true
N 3 ---> true