Question

Write the properties used, in order to solve the equation at each step. -1/3(6x-21)=-5(x+1)-2x+7=-5x-5-2x+5x+7=-5x-5x-53x+7-7=-5-73×/3=-12/3x=-4

Answer 1

`(-1)/(3)(6x-21)=-5(x+1)`

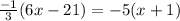
Open the bracket on LHS by multiplying with -1/3 and RHS by multiplying with -5 with quantity inside the bracket.

`\begin{gathered} (-1)/(3)*6x-((-1)/(3)*21)=-5* x+(-5)*1 \\ -2x-(-7)=-5x-5 \\ -2x+7=-5x-5 \end{gathered}`

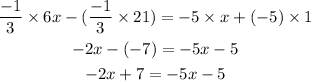
Add '5x' to LHS (Left-hand side) and RHS (Right-hand side) of the above expression to eliminate the 5x in the RHS.

`\begin{gathered} -2x+7+(5x)=-5x-5+(5x) \\ (-2x+5x)+7=(-5x+5x)-5 \\ 3x+7=0x-5 \\ 3x+7=-5 \end{gathered}`

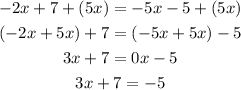
Substract '7' from both RHS and LHS of the above expression.

`\begin{gathered} 3x+7-(7)=-5-(7) \\ 3x+0=-12 \\ 3x=-12 \end{gathered}`

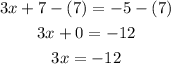
Divide '3' from the RHS and LHS of the above expression.

`\begin{gathered} (3x)/(3)=(-12)/(3) \\ x=-4 \end{gathered}`

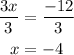
Thus, the value of x is -4.