Question

Please help me with this problem I am not able to help my son to understand we keep getting it wrong please help.A community recreational center has 500 ft of fencing with which to enclose a rectangular parking lot in the back of the property. The building itself will be used as one of the sides of the enclosed area. What is the maximum area that can be enclosed by the fencing?Enter your answer in the box. ft²

Answer 1

If one of the sides of the park is the building itself then, only three sides of the park will be enclosed by fencing of 500ft. See illustration below.

So, if only three sides of the building are to be fenced and we have 500ft available for fencing, then we can say that:

`w+w+l=500ft`

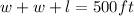
The equation above can be also written as:

`\begin{gathered} 2w+l=500ft_{} \\ or \\ l=500ft-2w \end{gathered}`

This will be our equation 1: l = 500ft - 2w.

Moving on to the area, the formula in getting the area of a rectangle is:

`A=l* w`

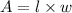
Using the value of "l" or length in equation 1, let's plug it into the formula of the area.

`A=(500-2w)* w`

Then, simplify by multiplying the outer w to the terms inside the parenthesis.

`\begin{gathered} A=500w-2w^2 \\ \text{Rearrange.} \\ A=-2w^2+500w \end{gathered}`

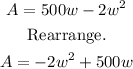
Now, to determine what value of "w" or "width" would give us the maximum area, we need to find the x-coordinate of the vertex of the quadratic equation above.

The formula is:

`x=-(b)/(2a)`

The quadratic equation above is in a general form ax² + bx + c where a = -2 and b = 500. So, plugging these values to the formula above, we get:

`x=-(500)/(2(-2))\Rightarrow x=-(500)/(-4)=125`

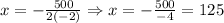
Hence, the x-coordinate of the vertex of the quadratic equation is 125. Therefore, to get a maximum area, the measurement of the width must be 125 ft.

To determine the maximum area, let's plugin w = 125 to the quadratic equation.

`\begin{gathered} A=-2w^2+500w \\ A=-2(125)^2+500(125) \\ A=-2(15,625)+62,500 \\ A=-31,250+62,500 \\ A=31,250ft^2 \end{gathered}`

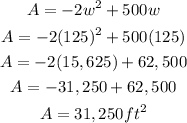
Therefore, the maximum area that the 500ft of fencing can enclose is 31, 250ft².