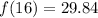Question

If f(x)is an exponential function where f(2.5)=13 and f(9.5)=20, then find the value of f(16) to the nearest hundredth.

Answer 1

Step-by-step explanation:

The general form of an exponential funtion isgiven below as

`y=ab^x`

From the question, the two points given are

`\begin{gathered} (2.5,13) \\ (9.5,20) \end{gathered}`

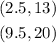
Step 1:

Put x=2.5 and y=13 to get equation 1

`\begin{gathered} y=ab^x \\ 13=ab^(2.5)----(1) \end{gathered}`

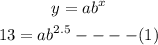
Step 2:

Put x=9.5 and y=20 get equation 2

`\begin{gathered} y=ab^x \\ 20=ab^(9.5)-----(2) \end{gathered}`

Step 3:

Divide equation (2) by (1)

`\begin{gathered} (20)/(13)=(ab^(9.5))/(ab^(2.5)) \\ b^7=(20)/(13) \\ b=\sqrt[7]{(20)/(13)} \end{gathered}`

Sustitute b in equation 1

`\begin{gathered} 13=ab^(2.5) \\ a=\frac{13}{(\sqrt[7]{(20)/(13))^(2.5)}} \\ a=11.146 \end{gathered}`

Step 4:

Find y when x=16

`\begin{gathered} y=ab^x \\ y=11.146(\sqrt[7]{(20)/(13))^(16)} \\ y=29.84 \end{gathered}`

Hence,

The final answer is

`f(16)=29.84`