Question

Drag the tiles to the correct boxes to complete the pairs. Match each point of intersection with the system of equations whose solution is at that point.

Answer 1

To determine which point is a solution to which equation system, you have to identfy which line corresponds to which equation and the coordinates of each point.

Points

W (≈-7/3,≈4/3)

X (-1,3)

Y (1,1)

Z (≈-1/2,-2)

The symbol ≈ indicates that is an approximate value.

Brown line

Has y-intercept at (0,-3)

And slope

Using points (0,-3) and (-1,-1)

`m=(-3--1)/(0--1)=-(2)/(1)=-2`

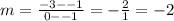
Its equation is y=-2x-3

Blue line

Has y-intercept (0,2)

And slope

Using points (0,2) and (-1,-3)

`m=(2-3)/(0--1)=-1`

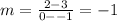
Its equation is y=-x+2

Red line

Has y-intercept (0,4)

And slope

Using points (0,4) and (-1,-3)

`m=(4-3)/(0--1)=1`

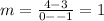
Its equation is y=x+4

Black line

Has y-intercept (0,-1)

And slope

Using points (0,-1) and (1,1)

`m=(1-(-1))/(1-0)=2`

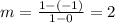
The equation for this line is y=2x-1

The first equation system is

y=-2x-3

y=2x-1

Corresponds to the intersection between the brown and black lines. The point that is a solution for this system is Z

The second equation system is

y=x+4

y=-x+2

Corresponds to the intersection between the blue and red lines. The point that is a solution for this system is X

The third equation system is

y=-2x-3

y=x+4

Corresponds to the intersection between the brown and red lines. The point that is a solution for this system is W

The fourth equation system is

y=2x-1

y=-x+2

Corresponds to the intersection between the black and blue lines. The point that is a solution for this system is Y

Another way for solving this exercise is by calculating the solution of each system and placing the results in the grid. For example for the first system:

y=-2x-3

y=2x-1

`-2x-3=2x-1`

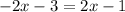
solve for x

`\begin{gathered} -2x-2x-3=2x-2x-1 \\ -4x-3+3=-1+3 \\ -4x=2 \\ -(4x)/(-4)=(2)/(-4) \\ x=-(1)/(2) \end{gathered}`

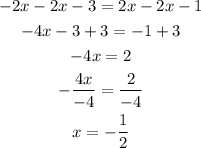
And now replace this value in one of the equations

`\begin{gathered} y=-2(-(1)/(2))-3 \\ y=-2 \end{gathered}`

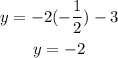
The solution for this system is (-1/2,-2) → If you look at the coordinates determined above, you'll see that these correspond to point Z

Both ways are equally valid to determine which point corresponds to each system.