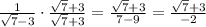Question

Evaluate the integral. Please.

Answer 1

`\tan\theta + \sec\theta + C`

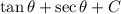
Explanation:

This cool problem uses an old trick: multiplying by a cleverly chosen expression for 1 (a fraction with the same numerator and denominator).

`\int (\sec\theta)/(\sec\theta-\tan\theta) \cdot (\sec\theta+\tan\theta)/(\sec\theta+\tan\theta)\, d\theta\\\\=\int(\sec\theta(\sec\theta+\tan\theta))/(\sec^2\theta-\tan^2\theta)`

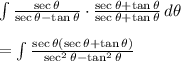
That denominator looks kind of familiar. Remember one of the so-called Pythagorean identities?

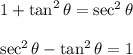`1+\tan^2\theta=\sec^2\theta\\\\\sec^2\theta - \tan^2\theta =1` The denominator of the integrand is just 1 !!!

The integral is now

`\int \sec\theta(\sec\theta+\tan\theta) \, d\theta = \int(\sec^2\theta+\sec\theta\tan\theta) \, d\theta\\=\int \sec^2\theta \, d\theta + \int \sec\theta\tan\theta \, d\theta\\=\tan\theta + \sec\theta + C`

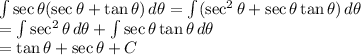
That little trick is good to know. You may have used it before to rationalize a denominator. Example:

`(1)/(√(7)-3)\cdot(√(7)+3)/(√(7)+3)=(√(7)+3)/(7-9)=(√(7)+3)/(-2)`