We can represent the situation using the following drawing:
Now, we can see that we have a right triangle, and we can find the distance using the Pythagorean Theorem as follows:
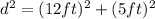
Now, we have:

If we take the square root to both sides of the equation, we will have:
![\sqrt[]{d^2}=\sqrt[]{169ft^2}\Rightarrow d=13ft](https://img.qammunity.org/2023/formulas/mathematics/college/vhlu79695hpg9zmj0mc54gtr6fgy1cuxjh.png)
In summary, therefore, the distance from Adrian's location on the ground to the top of the tree is 13ft (Second Option).