The motion of the golf ball is a projectile motion.
The horizontal distance the ball travels before striking the ground again is the range.
The formula to calculate range is;
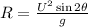
where U = initial velocity = 148 ft/s
1 foot = 0.3048m
148 ft/s = 148 x 0.3048 = 45.11
Hence, U = 45.11 m/s

Therefore the range is;
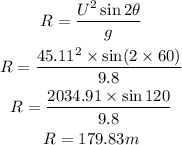
The range is 179.83m
In feet, it will be;
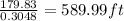
Therefore, to the nearest tenth, the ball lands 590.0 feet or 179.8m from the golfer after being struck.