Question

The length of a rectangle is 1 yard more than twice the width, and the area of the rectangle is 45 Yard^2. What is the Length=What is the Width=

Answer 1

Step-by-step explanation

Let's make a drawing of the problem:

We have a rectangle and some relations between its length and its width, and we want to find the value of each of them.

Firstly, let's express the relations between the length and the width as equations. To do that, we need to define

L:= Length,

W:= Width.

Then, we get the system

`\begin{cases}L=1+2W, \\ L\cdot W=45.\end{cases}`

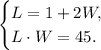
The first equation says that the length (L) is one yard more than twice (to multiply by two) the width (W). And the second one says that the area of the rectangle, which can be calculated by multiplying the length and the width, is 45 yd^2.

Now, our task is to solve the system above. Replacing the "value" of L given by the first equation, in terms of W, into the second equation, we get

`\begin{gathered} (1+2W)W=45, \\ W+2W^2=45, \\ 2W^2+W-45=0. \end{gathered}`

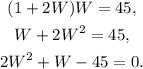
The last equality is a polynomial equation of degree 2. Let's recall the general solution of such an equation: If we have a polynomial equation of the form

`ax^2+bx+c=0,`

its solution(s) is(are) given by

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\text{.}`

Applying this to our polynomial equation, we get

`\begin{cases}a=2 \\ b=1 \\ c=-45\end{cases}\Rightarrow x=\frac{-1\pm\sqrt[]{1^2-4(2)(-45)}}{2(2)}=\frac{-1\pm\sqrt[]{361}}{4}=(-1\pm19)/(4)\text{.}`

Then, we have two solutions

`\begin{gathered} x_1=(-1+19)/(4)=(18)/(4)=(9)/(2), \\ x_2=(-1-19)/(4)=(-20)/(4)=-5. \end{gathered}`

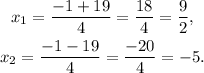
However, note that the second solution is negative, and negative lengths exist (make no sense). Then, the width of our rectangle is 9/2.

Having found the value of W, we can easily find the value of L by the first equation:

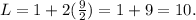
`L=1+2((9)/(2))=1+9=10.`Answer

The width of the rectangle is 9/2 yd.

The length of the rectangle is 10 yd.