Notice that the parent function of f(x) is:
![g(x)=\sqrt[3]{x}.](https://img.qammunity.org/2023/formulas/mathematics/college/4e79ymqa6x9de7re3yh7rytqistqj5vz2u.png)
Now, to determine the transformations, we recall the following:
The graph of a function h(x)
1.- horizontally translated n units to the left is represented by the following function:
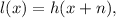
2.- vertically translated down m units:
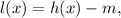
3.- reflected over the x-axis:
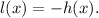
Therefore, f(x) is g(x) translated 2 units to the left, reflected over the x-axis, and translated 4 units down.
To determine 5 points on the graph, we evaluate the graph at x=-2, x=6, x=-10, x=-1, x=-3, and get:
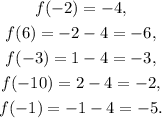
Therefore, the points (-2,-4),(6,-6),(-3,-3),(-10,-2),(-1,-5) are on the graph.
Answer:
f(x) is
![g(x)=\sqrt[3]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/lo1sya7fzgu08qbq0i3fx965ovrmasphsr.png)
translated 2 units to the left, reflected over the x-axis, and translated 4 units down.
5 points on the graph:
(-2,-4),(6,-6),(-3,-3),(-10,-2),(-1,-5).