Answer:
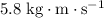 .
.
Step-by-step explanation:
If the mass of an object is
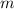 and the velocity of that object is
and the velocity of that object is
 , the linear momentum of that object would be
, the linear momentum of that object would be
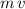 .
.
Assume that the initial velocity of the mass is positive (
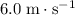 .) However, the direction of the velocity is reversed after the impact. Thus, the sign of the new velocity of the object would be negative- the opposite of that of the initial velocity. The new velocity would be
.) However, the direction of the velocity is reversed after the impact. Thus, the sign of the new velocity of the object would be negative- the opposite of that of the initial velocity. The new velocity would be
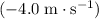 .
.
Thus, the change in the velocity of the mass would be:
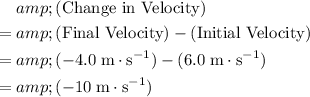 .
.
The change in the linear momentum of the mass would be:
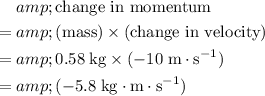 .
.
Thus, the magnitude of the change of the linear momentum would be
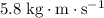 .
.