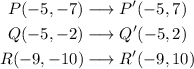The transformation rule for a reflection across the x-axis is:
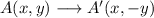
We will apply this rue to the three vertices.
Reflection across the x-axis of P:
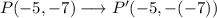
In the image point, the x-coordinate remains the same, but we have to change the sign of the y-coordinate:

Reflection across the x-axis of Q:
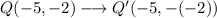
Simplifying the expression:

Reflection across the x-axis of R:
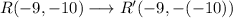
simplifying the expression:

Answer: