Question

Determine whether f(x)=1/2 x-4x+8 has a minimum or maximum value and find the value

Answer 1

The function has a minimum

The minimum value is zero

Explanations:

Given the quadratic function expressed as shown below:

`f(x)=(1)/(2)x^2-4x+8`

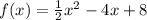
We are to determine if the function has a minimum or maximum value.

Step 1: Find the critical points of the function. At turning point f'(x) = 0.

`\begin{gathered} f^(\prime)(x)=(2)/(2)x^(2-1)-4x^(1-1) \\ f^(\prime)(x)=x-4 \end{gathered}`

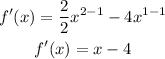
Equating the function to zero to get the critical point(s)

`\begin{gathered} x-4=0 \\ x=4 \end{gathered}`

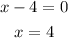
Step 2: Determine the second derivative of the function:

`\begin{gathered} f^(\prime)(x)=x-4 \\ f^(\doubleprime)(x)=1 \end{gathered}`

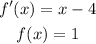
Since f''(x) > 0, hence the function given is at the minimum.

Determine the minimum value of the function by substituting x = 4 into the original function.

`\begin{gathered} f(4)=(1)/(2)(4)^2-4(4)+8 \\ f(4)=(16)/(2)-16+8 \\ f(4)=8-16+8 \\ f(4)=0 \end{gathered}`

Hence the minimum value of the function is zero