Recall the trigonometric function tangent.
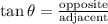
We can use either 30° or 60° as our basis for the angle. In this case, we will use 60° (using 30° works just as well, we just have to determine its corresponding opposite and adjacent sides)
![\begin{gathered} \text{Given} \\ \theta=60\degree \\ \text{opposite to }\theta=x \\ \text{adjacent to }\theta=\sqrt[]{8} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fwpaft1ky0ujzdv9qzxy7f9632hz4a6dec.png)
Substitute these values to the tangent function and we have
![\begin{gathered} \tan \theta=\frac{\text{opposite}}{\text{adjacent}} \\ \tan 60\degree=\frac{x}{\sqrt[]{8}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q42kat00p7pr5m5socd7gcbqiy36oz9le0.png)
Multiply both sides with square root of 8, to get rid of the fraction in the right side.
![\begin{gathered} \sqrt[]{8}\cdot\tan 60\degree=\frac{x}{\sqrt[]{8}}\cdot\sqrt[]{8} \\ \sqrt[]{8}\cdot\tan 60\degree=\frac{x}{\cancel{\sqrt[]{8}}}\cdot\cancel{\sqrt[]{8}} \\ \sqrt[]{8}\cdot\tan 60\degree=x \\ \\ x=\sqrt[]{8}\cdot\tan 60\degree \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yoir75yto5asp5atsm1ithb59ckw5kr0yh.png)
Recall that tan 60° = square root of 3 therefore
![\begin{gathered} x=\sqrt[]{8}\cdot\tan 60\degree \\ x=\sqrt[]{8}\cdot\sqrt[]{3} \\ x=\sqrt[]{8\cdot3} \\ x=\sqrt[]{24} \\ x=\sqrt[]{4\cdot6} \\ x=2\sqrt[]{6} \\ \\ \text{Therefore, the value of }x\text{ is }2\sqrt[]{6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wma2r6i9mvhoukraxzowojhkk5abeig9xe.png)