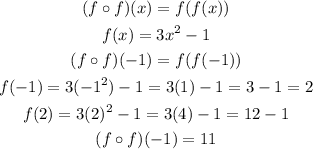SOLUTION
Given the question in the question tab, the following solution steps answer the questions
Step 1: Write the given functions
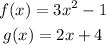
Step 2: Find f(g(2))

The composite function f(g(2)) will give 191
Step 3: Find f(g(x))
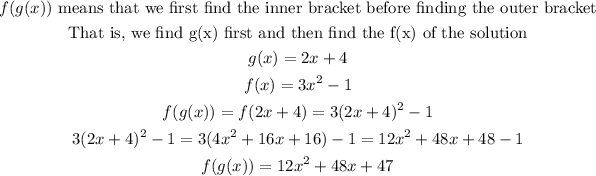
Step 4: Find g(f(x))
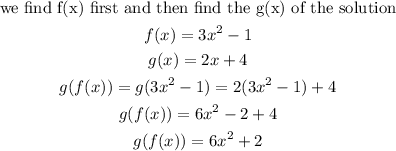
Step 5: Find (gog)(x)
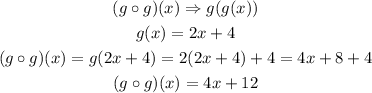
Step 6: Find (fof)(-1)