1 Answer

Lakenya · Answer 1 · 2023-06-16T08:18:48+0000

Step-by-step explanation:

Given that

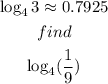
$\begin{gathered} \log_43\approx0.7925 \\ find \\ \log_4((1)/(9)) \end{gathered}$

Apply the law of fractional indices below

By applying the law, we will have that

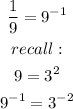
$\begin{gathered} (1)/(9)=9^(-1) \\ recall: \\ 9=3^2 \\ 9^(-1)=3^(-2) \end{gathered}$

By rewriting the expression, we will have

$\operatorname{\log}_4((1)/(9))=\log_4(3^(-2))$

Apply the logarithmi law of exponents below

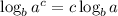
$\log_ba^c=c\log_ba$
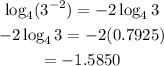
$\begin{gathered} \log_4(3^(-2))=-2\log_43 \\ -2\log_43=-2(0.7925) \\ =-1.5850 \end{gathered}$

Hence,

The final answer to 4 decimal places is

$How do I evaluate a log when the argument is in a fraction?-example-1$

Please log in or register to add a comment.