We are given that the stress on a pipe varies directly with the internal pressure and internal diameter and inversely with the thickness. This means that the relationship between the variables is as follows:
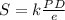
Where:

Now, we determine the value of "k" using the data provided:
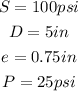
Now, we plug in the data:
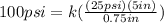
Now, we solve for "k". First, we solve the operations:
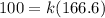
Now, we divide both sides by 166.6:
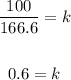
Therefore, the function is:
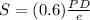
Now, we determine the value of "S" for the following data:
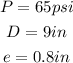
Now, we plug in the data:
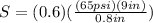
Solving the operations:

Therefore, the stress is 438.750 pounds per square inch.