Given the information on the problem, we can write the following system of equations:
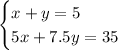
then, we can write the following augmented matrix:
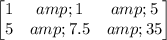
now, if we multiply by 5 the first row and then substract it from the second row, we get:

notice that from the second equation, we can find the value of y:
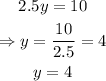
now that we have that y = 4, we can use this value on the first equation to find x:
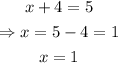
now, we have that the babysitter worked 1 hour before 11pm and 4 hours after 11 pm,then, the Burkes came home at 3 am