Question

A car starts from rest and travels for 5.6 s with a uniform acceleration of +1.8 m/s2. The driver then applies the brakes, causing a uniform acceleration of -1.7 m/s2. The breaks are applied for 1.70 s.a) How fast is the car going at the end of the braking period?(b) How far has the car gone from its start?

Answer 1

Given:

Time = 5.6 s

Aceleration = 1.8 m/s²

Decceleration when the brakes are applied = -1.7 m/s²

Duration the brake wes applied = 1.70 s

Let's find the following:

(a) Speed of the car at the end of the braking period.

First find the distance travelled in the first 5.6 seconds.

`\begin{gathered} d_1=ut+(1)/(2)at^2 \\ \\ d1_{}=0(5.6)+(1)/(2)\ast1.8\ast5.6^2 \\ \\ d1_{}=0+(1)/(2)\ast1.8\ast31.36 \\ \\ d1_{}=28.22\text{ m} \end{gathered}`

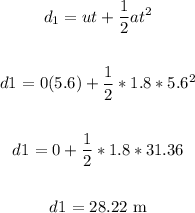
Now, find the velocity travelled in the first 5.6 seconds:

`\begin{gathered} v_1=u+at \\ \\ v_1=0+1.8(5.6)=10.08\text{ m/s} \end{gathered}`

Let's find the velocity after applying the brakes for 1.70 seconds:

Where:

u = 10.08 m/s ( the final velocity of the acceleration is the initial velocity at the start of the braking period).

a = -1.7 m/s^2

t = 1.70 m/s

`\begin{gathered} v_2=u+at \\ \\ v_2=10.08+(-1.7)(1.7) \\ \\ v_2=10.08-2.89=7.19\text{ m/s} \end{gathered}`

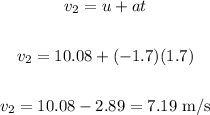
The velocity at the end of braking period is = 7.19 m/s

Therefore, the speed of the car at the end of the braking period is 7.19 m/s.

(b) DIstance the car has gone from its start.

To find the distance the car has gone from its start, find the distance covered in 1.7 seconds when the brake was applied.

`\begin{gathered} d_2=ut+(1)/(2)at^2 \\ \\ d_2=10.08(1.7)+(1)/(2)(-1.7)(1.7)^2 \\ \\ d_2=14.68\text{ m} \end{gathered}`

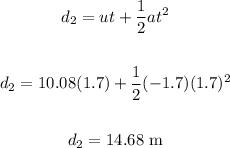
Therefore, the total distance covered is:

Total distance = 28.22 m + 14.68 m = 42.9 meters

Therefore, the distance the car has gone from its start is 42.9 meters.