, the answer is 2020 kV
Step-by-step explanationElectric potential of a point charge is
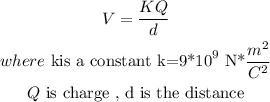
so
Step 1
Diagram:
Step 2
distances:fromthe center to each charge:
:
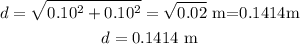
Step 3
electric potential due to each charge.
a) Q1
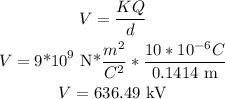
b)Q2
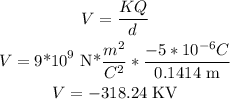
c)Q3
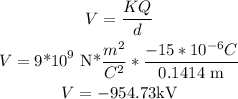
d)Q4
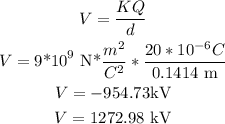
so, the resultant electric potential are:
:
So
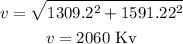
therefore, the answer is 2020 kV
I hope this helps you