Question

Find the coordinates of the point on a circle with radius 20 corresponding to an angle of 120o . If your answer is not an integer then round it to the nearest hundredth. The x component of the coordinate is AnswerThe y component of the coordinate is Answer

Answer 1

Let us draw a sketch to understand the question

We need to find the coordinates of the point (-x, y)

Since cos(60) = adjacent/hypotenuse

Since the adjacent = x

Since the hypotenuse = 20, then

`cos\left(60\right)=(x)/(20)`

By using the cross-multiplication

`x=20cos\left(60\right)`

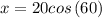
Since x must be negative

Since cos(60) = 0.5, then

`\begin{gathered} x=-20\left(0.5\right) \\ x=-10 \end{gathered}`

Since sin(60) = opposite/hypotenuse

Since the opposite = y

Since the hypotenuse = 20, then

`sin\left(60\right)=(y)/(20)`

By using the cross multiplication, then

`\begin{gathered} y=20sin\left(60\right) \\ y=20\left((√(3))/(2)\right? \\ y=10√(3) \end{gathered}`

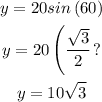
Change it to decimal and round it to the nearest hundredth, then

`y=17.32`

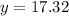
The x component of the coordinates is -10

The y component of the coordinate is 17.32