Question

i dont know how to draw the graph as explained. Im actually confused about mostly all of it. I only know how domain and range works and how to tell if its a function.

Answer 1

1- You can draw the first line starting at (0,0) and make it as a straight line.

2-

3-

Slope:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \\ m=(7-0)/(8-0)=(7)/(8) \end{gathered}`

4- As the line starts in (0,0) the y-intercept (b) is 0, then the equation of the line

(y=mx+b) is:

`y=(7)/(8)x`

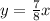
5- Domain: All values of x where the function is defined:

`\lbrack0,38\rbrack`

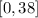
Range: All values that the function takes (y-values):

`\lbrack0,9.7\rbrack`

6-

Rate of change;

`\frac{f(end)-f(top)}{xend-\text{xtop}}`

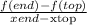
First hill:

`(4-7)/(11-8)=-(3)/(3)=-1`

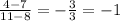
Second hill:

`(5-9.7)/(20-16)=-(4.7)/(4)=-1.175`

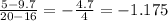
Third hill:

`(4.2-6)/(37-34)=-(1.8)/(3)=-0.6`

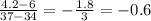
The greater the rate of change the steeper the hill.

Then, the steeper hill is number 3 (.-0.6 is greather than -1 and -1.175)

7-Draw vertical lines in different parts of the graph, if a vertcal line touches the graph at more than one point then the graph is not a function ( a value of x can not have two different values of y)

It is not a function