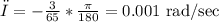Given a figure represents the distance between an airplane and a radar station on the ground.
We will find the following:
Step 1: we will find a relation between x and θ
As shown we may consider the triangle which a right-angle triangle
With the height = 3000 ft
And the side (x) is the adjacent side to the angle θ
the side (3000) is the opposite side to the angle θ
so, we can write the following equation:
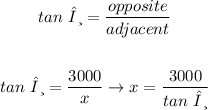
Step (2): at the instant x = 2000 ft, we will compute the following:
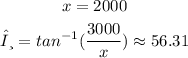
Also, we will find the first derivative of x and θ
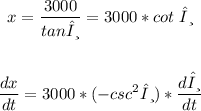
the value of (dx/dt) is given and equal to 200 ft/sec
Substitute dx/dt and θ to find dθ/dt
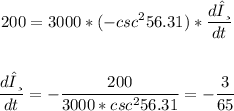
So, the answer to step (2) will be as follows:
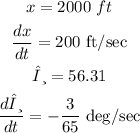
Step (3):
We will find how fast the radar is rotating
Which will be the angular velocity ω
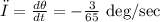
convert from degree to radian