To find the volume of the sphere use the following formula:
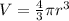
Where V is the volume and r is the radius. Use the given diameter to find the radius (radius is half the diameter):
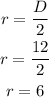
Now, use this value to find the volume of the sphere:
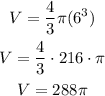
The answer is 288pi in^3.
The approximate volume would be:
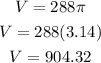
The approximate volume is 904.32, rounded to the nearest cubic inch it is 904.