Question

The angle below measures 5 radians, and a circle is centered at the angle's vertex.The x-coordinate of the terminal point is 0.28. What is the y-coordinate of the terminal point?y=

Answer 1

Trigonometric Functions

The sine and cosine functions are defined as the vertical and horizontal projections of the coordinates of the terminal points respectively.

If x is the projection of the terminal point on the x-axis and y is the projection of the terminal point on the y-axis, then:

`r^2=x^2+y^2`

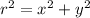
Where r is the radius of the circle.

If we are given the value of the angle θ, then:

x = r cos θ

y = r sin θ

We are given the angle of the terminal point θ=5 radians and the x-coordinate of its terminal point as x=0.28

Solving the equation for r:

`r=(x)/(\cos\theta)=(0.28)/(\cos 5)=0.9871`

Now we find the value of y

y = r sin 5

y = 0.9871 * (-0.9589) = -0.9465

The y-coordinate of the terminal point is y = -0.9465