Let's begin by listing out the information given to us:
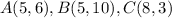
A scale factor of 1/3 means the triangle will be smaller (reduction):
![\begin{gathered} P=(2,3) \\ AB=4\Rightarrow A^(\prime)B^(\prime)=(4)/(3) \\ BC=\sqrt[]{58}\Rightarrow B^(\prime)C^(\prime)=\frac{\sqrt[]{58}}{3} \\ AC=\sqrt[]{18}\Rightarrow A^(\prime)C^(\prime)=\frac{\sqrt[]{18}}{3}=\sqrt[]{6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dxpvhp8u9nd27d1cggmonflxucwgcbkklx.png)
A scale factor of 2 means the triangle will be bigger (enlargement):
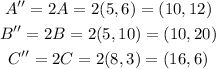
Both triangles are similar; while the first is a reduction, the second is an enlargement