Zeros: -7/3, 1; y-intercept: (0,-7) ;minimum: -8.3
1) Considering the quadratic function y=3x²+4x-7, we can find their zeros by solving it:
![\begin{gathered} y=3x^2+4x-7 \\ x=\frac{-b\pm\sqrt[]{\Delta}}{2a}=\frac{-4\pm\sqrt[]{(16)-4(3)(-7)}}{2(3)}= \\ x_1=1 \\ x_2=-(7)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yktc37ckmy1diegnw1xm7zx9adjbdialeh.png)
Note that the zeros can also be called "roots" and since the parabola hits the x-axis twice we have two Real roots.
2) Let's continue. Looking at the function we can state that the y-intercept is given by the number -7, or the coefficient "c". As a point, we have (0,-7) as the y-intercept
2.2) We can also find the minimum by using this formula since a >0:
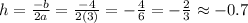
This is the x-coordinate of the minimum. We need to plug into the function to get the y-coordinate:
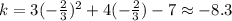
So the minimum point is located at (-0.7, -8.3)
3) Hence, the answer is:
Zeros: -7/3, 1; y-intercept: (0,-7) ;minimum: -8.3