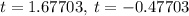We are given the equation
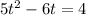
To solve this question using the quadratic formula
We will re-write the equation as follow:
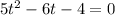
Next, we will compare with the general quadratic formula

In our case
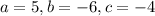
To apply the quadratic formula
![t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/3cgw61gskglny4a505tle5b9wokluktv58.png)
What we will do next will be to substitute the values of a,b, and c
![t=\frac{-(-6)\pm\sqrt[]{(-6)^2-4*5*-4}}{2*5}](https://img.qammunity.org/2023/formulas/mathematics/college/o3ib59wwtckf6za65hxqs1oe9u8tahbbzt.png)
![t=\frac{6\pm\sqrt[]{36+80}}{10}](https://img.qammunity.org/2023/formulas/mathematics/college/7errn0f4tpihsftkxnvwa2x68jjntyvc94.png)
![t=\frac{6\pm\sqrt[]{116}}{10}](https://img.qammunity.org/2023/formulas/mathematics/college/gmuhpphsjhpqd2jck3a2fe7rtk5s3zokfj.png)
![t=\frac{6\pm2\sqrt[]{29}}{2*5}](https://img.qammunity.org/2023/formulas/mathematics/college/bl1t5a1ortn7pd2l872wbcp2i37hvbfdvn.png)
Simplifying further
![\begin{gathered} t=\frac{6+2\sqrt[]{29}}{2*5},t=\frac{6-2\sqrt[]{29}}{2*5} \\ \\ t=\frac{3+\sqrt[]{29}}{5},t=\frac{3-\sqrt[]{29}}{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4z1rtg9wgsmn8oocf2jxyjtlm5e5x8et5s.png)
If we are to get the values in decimals, the value of t will be