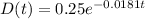Question

1. The recommended starting dosage used for treating congestive heart failure for most patients is 0.25mg of digoxin, once daily. The mean half-life for digoxin elimination is about 1.6 days or 38.4 hours in individuals whose renal and hepatic function are normal. This means the amount of digoxin will be eliminated from the body at an average rate of 1.79% per hour.A) Is this function increasing or decreasing? Explain.B) What is the percent rate of change per hour of digoxin in a patient's body who is going through digoxin therapy?C) What is the decay factor per hour? Round decimal to four placesD) Write an exponential model for the amount of digoxin in the body, D(t), measured in mg, as afunction of time, t, hours since the initial dosage.

Answer 1

A)

This function is decreasing, this comes from the fact that the amount of digoxin on the body is getting smaller as time goes by.

B)

We know that the decay factor is 0.0181; this means that for every hour it passes the the percent decreases by 1.81%

C)

The decay factor is related to the galf life by the equation:

`t_{(1)/(2)}=(\ln 2)/(\lambda)`

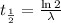
then we have;

`\begin{gathered} \lambda=\frac{\ln 2}{t_{(1)/(2)}} \\ \lambda=(\ln 2)/(38.2) \\ \lambda=0.0181 \end{gathered}`

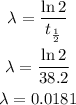
Therefore the decay factor is 0.0181.

D)

The exponential model of a decay is given by:

`D(t)=N_0e^(-\lambda t)`

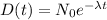
where N0 is the initial quantity, therefore in this case we have:

`D(t)=0.25e^(-0.0181t)`